A force is a push or a pull that alters the state of motion of a body and is measured in Newtons (N). As explained in Newton’s first law of motion a force is required to make a stationary body move, change speed, direction or stop.
In sport, an internal force is one which is generated within the body which could be, for example, the leg muscles contracting to move the bones. An external force is one that acts outside the body, for example, a boxer striking their opponent.
Here are some examples of forces acting on a baseball player. Force is a vector quantity which means it needs BOTH magnitude (size) and direction. To get a better understanding of the forces acting in a particular situation we can draw arrows to indicate the direction the forces are acting. To do this we need three pieces of information:
- The point in which the force is applied.
- The direction of the force.
- The size or magnitude of the force.
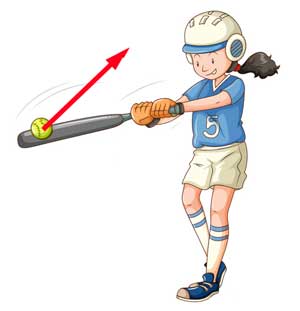
The red arrow in the diagram above indicates the point at which the force acts, the direction and the size. If the force was bigger we could use a larger arrow.
Net force
The net force is the sum of all the forces acting on a body. If the forces are balanced then the net force is zero and the body will not move (or change velocity). If the forces are not balanced (the net force is non zero) the body will move in the direction of the net force.
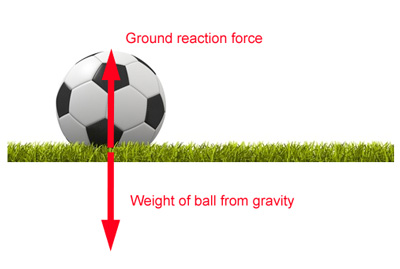
Balanced forces
In the diagram below the ball is stationary because the forces acting on it are balanced.
Unbalanced forces
In the diagram below the forces on the blue fighter are not balanced. The force of foot on the face is much greater than any resisting forces from the muscles of the blue fighter. Friction forces on the ground prevent the blue player from sliding. Gravity also acts on both fighters.
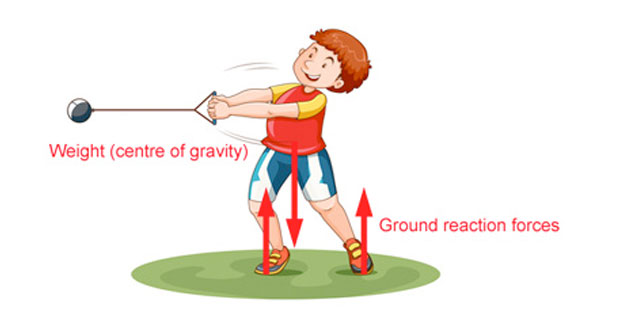
Vertical forces
The vertical forces acting on athletes are weight (mass x acceleration due to gravity) and the ground reaction force. In the diagram below, the vertical forces are weight (acting downwards from the centre of gravity) and the ground reaction forces acting up at the contact points of the feet. There are other rotational forces acting here but we are only considering the vertical forces for now.